SAT趣味数学：探索勾股定理

　　SAT的数学考试对于中国学生而言十分简单，甚至把勾股定理，怎么求三角形的面积和周长也印在卷子上，怕学生忘记而不会答题。对我们中国学生而言，只需要有国内初中水平的数学底子，认真复习一下，考一个不错的分数还是较为容易的。不过对于喜欢探索数学的同学而言，未免有点扫兴，感觉只是展现了数学的皮毛，不甚畅快。下面大家就来一起探索一下勾股定理，体验数学的趣味吧。

　　a，b，c分别代表直角三角形的勾、股、弦三边之长

　　(a^2)+(b^2)=(C^2)

　　其变形b^2=c^2-a^2=(c-a)(c+a)

　　a^2=c^2-b^2=(c-b)(c+b)，

　　c^2=2ab+(b-a)^2

　　勾股定理

　　命题1 如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a^2+b^2=c^2

　　勾股定理的逆定理

　　命题2 如果三角形的三边长a，b，c满足a^2+b^2=c^2，那么这个三角形是直角三角形。

　　关于勾股定理，如何证明呢?

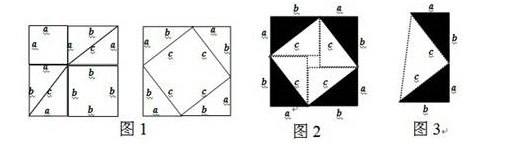
　　一、传说中毕达哥拉斯的证法(图1)

　　左边的正方形是由1个边长为a 的正方形和1个边长为b 的正方形以及4个直角边分别为 a、b ，斜边为 c的直角三角形拼成的。右边的正方形是由1个边长为c 的正方形和4个直角边分别为 a、b ，斜边为 c的直角三角形拼成的。因为这两个正方形的面积相等(边长都是a+b )，所以可以列出等式 化简得 。

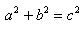　　在西方，人们认为是毕达哥拉斯最早发现并证明这一定理的，但遗憾的是，他的证明方法已经失传，这是传说中的证明方法，这种证明方法简单、直观、易懂。

　　二、赵爽弦图的证法(图2)

　　种方法：边长为 的正方形可以看作是由4个直角边分别为 a、 c，斜边为 c的直角三角形围在外面形成的。因为边长为 的正方形面积加上4个直角三角形的面积等于外围正方形的面积，所以可以列出等式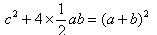 ，化简得 。

　　第二种方法：边长为 的正方形可以看作是由4个直角边分别为a 、b ，斜边为 的c直角三角形拼接形成的(虚线表示)，不过中间缺出一个边长为（b-a） 的正方形“小洞”。

　　因为边长为 的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积，所以可以列出等式 ，化简得 。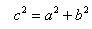

　　这种证明方法很简明，很直观，它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神，是我们中华民族的骄傲。

　　三、美国第20任总统茄菲尔德的证法(图3)

　　这个直角梯形是由2个直角边分别为 a、b ，斜边为c的直角三角形和1个直角边为c的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积，所以可以列出等式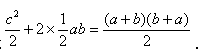 化简得 。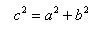

　　这种证明方法由于用了梯形面积公式和三角形面积公式，从而使证明更加简洁，它在数学史上被传为佳话。

　　以上就是给大家整理的探索勾股定理，你明白了吗?

相关阅读：